Testing Stuff

Testing out some of the common components I plan to use in future posts.

The singular value decomposition (SVD) of any rectangular matrix $\mathbf{A} \in \mathbb{C}^{m \times n}$ is of the form, $$ \mathbf{A} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^{*}, $$ where $\mathbf{U}$ is an $m \times m$ complex unitary matrix, $\mathbf{\Sigma}$ is an $m \times n$ diagonal matrix with nonnegative real numbers on the diagonal, and $\mathbf{v}$ is an $n \times n$ complex unitary matrix. Often the entries of $\mathbf{\Sigma}$ are ordered in a nonincreasing fashion and the columns of $\mathbf{U}$ and $\mathbf{V}$ are permuted accordingly. The SVD exists for all matrices and is an extremely useful factorization. It characterizes the range and null spaces of $\mathbf{A}$ and $\mathbf{A}^{*}$.

For real matrices $\mathbf{A} \in \mathbb{R}^{m \times n}$, the $\mathbf{U}$ and $\mathbf{V}$ factors become real orthogonal matrices and the SVD is written as $$\mathbf{A} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^{\sf T}.$$

The following figure taken from the Wikipedia article shows the SVD of a $2 \times 2$ matrix $\mathbf{M}$. The action of $\mathbf{M}$ on the unit disc is shown in the top figure, i.e., $\mathbf{M}\mathbf{x}$ for every $\lVert\mathbf{x}\rVert_2 = 1$. The canonical vectors $\mathbf{e}_1 = \begin{bmatrix}1\\ 0\end{bmatrix}$ and $\mathbf{e}_2 = \begin{bmatrix}0\\ 1\end{bmatrix}$ are shown in pink and yellow respectively.

The similar action is shown via the SVD of $\mathbf{M}$. First we rotate $\mathbf{x}$ by the unitary matrix $\mathbf{V}^*$ to form $\mathbf{V}^*\mathbf{x}$. Then stretch the coordinates via the diagonal matrix $\mathbf{\Sigma}$ before finally rotating via $\mathbf{U}$.

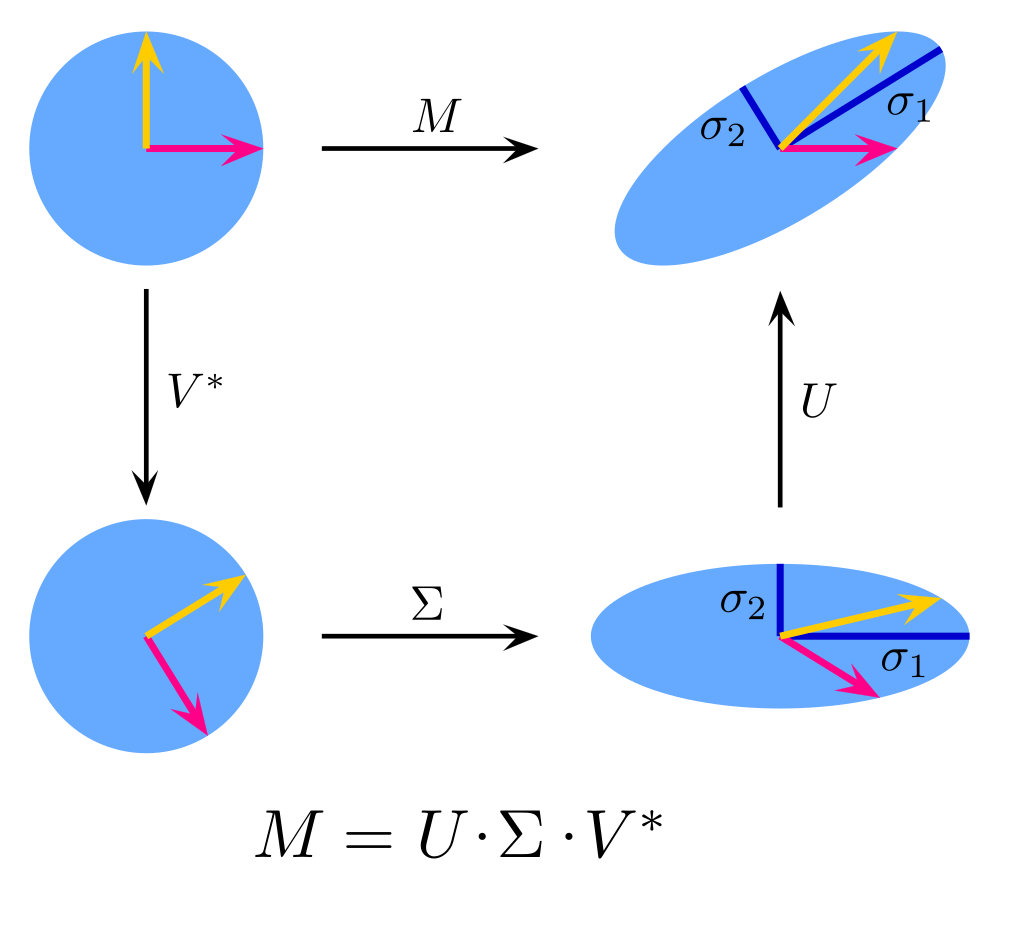
The SVD can be computed in Python by using the numpy function numpy.linalg.svd.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

import numpy as np

# Create a random m x n matrix
m, n = 10, 6
A = np.random.rand(m, n)

# Compute the SVD
U, s, Vt = np.linalg.svd(A)

# s is just a vector of singular values so create a diagonal matrix
S = np.zeros(m, n)
np.fill_diagonal(S, s)

# Check to see if the approximation is close
print(f"Approximation error: {np.linalg.norm(A-U.dot(S.dot(Vt))):.4f}")